
 |
|
|
Регистрация Восстановить пароль |
|||||||
| Регистрация | Задать вопрос |
Заплачу за решение |
Новые сообщения |
Сообщения за день |
Расширенный поиск |
Правила |
Всё прочитано |
||||
 |
|
|
|
Опции темы | Поиск в этой теме |
|
|
#91 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
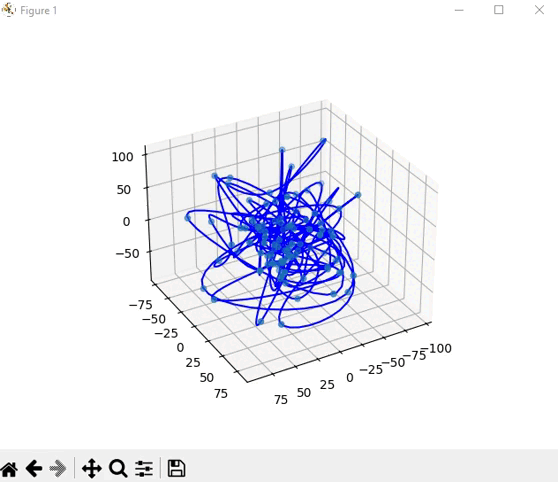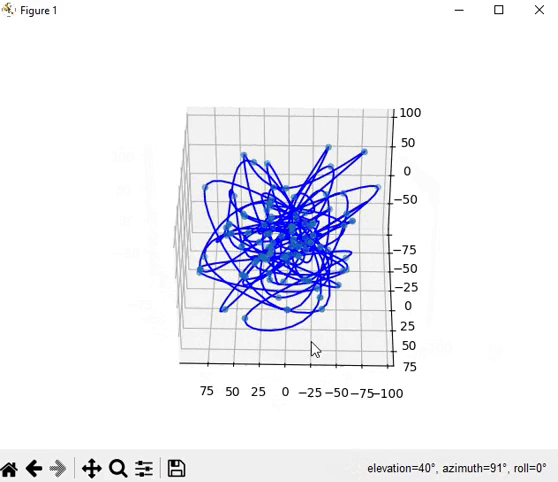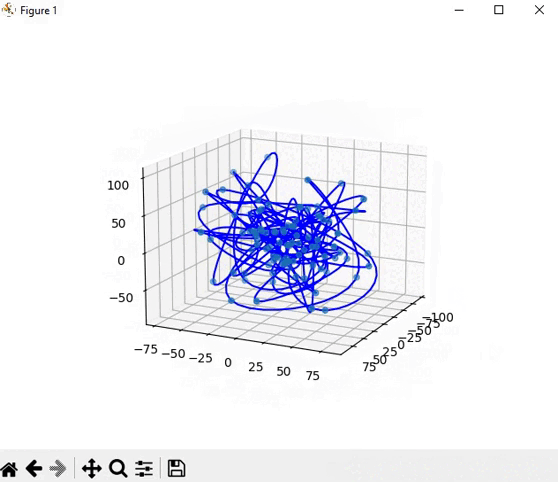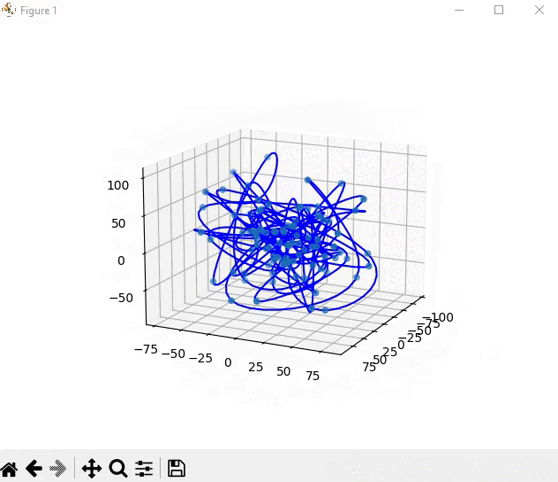
Но всё таки зона Долонгов это изогнутые линии а не кривые...
Код:
|
|
|

|
|
|
#92 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
TheMezzanine 2
Код:

|
|
|

|
|
|
#93 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
Процедурный генератор изогнутых склонов...
Код:
 Идеально подойдет для процедурной генераций каких нибудь подземелий гномов типа горы Эребор где есть такие пологие склоны 
Последний раз редактировалось MakarovDs; 27.10.2024 в 00:11. |
|
|

|
|
|
#94 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
Процедурный генератор обломков столбов
Код:

|
|
|

|
|
|
#95 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
Процедурный генератор обломков столбов БОЛЬШОЙ
Код:

|
|
|

|
|
|
#96 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
Процедурный генератор стен небоскребов
Код:
 Как раз подойдет для моего уровня -1000007 который удаляют некоторые пeдeрастическиe обезьянки на фандоме бэкрумса... Поэтому оставил описание на диске. Поэтому кстати ненавижу этот фандом закулисья написал свой эмоциональный порыв модератору он извинился, но потом всё равно удалил мой уровень ���� Какие же дуболомы! Непонимают что бэкрумс это мир бесконечностей где бесконечное число уровней! Там всевозможные вариаций размещений и сочетаний всевозможных пространств! Последний раз редактировалось MakarovDs; 27.10.2024 в 00:42. |
|
|

|
|
|
#97 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
Триангуляция Делоне но линиями
Код:
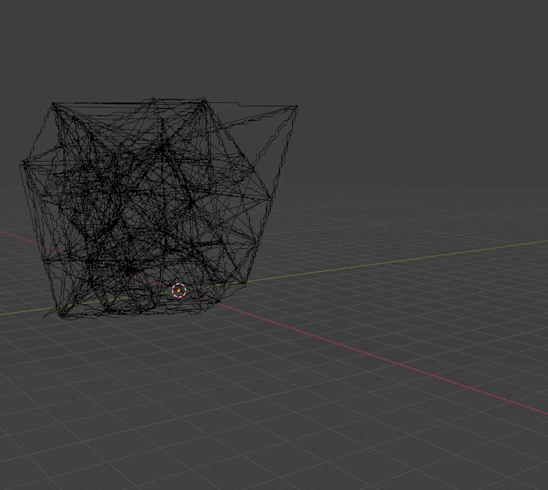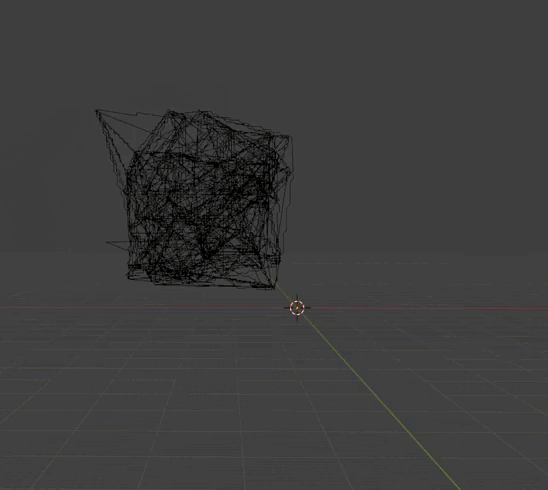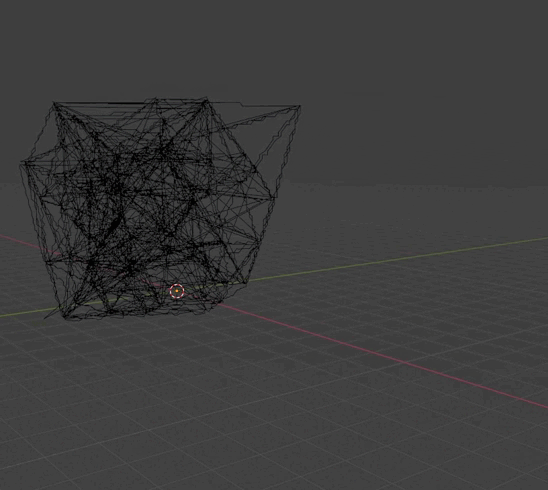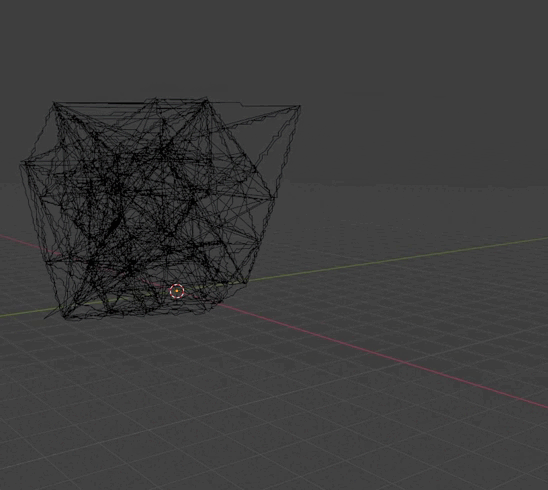
|
|
|

|
|
|
#98 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
���� ��������
Код:

|
|
|

|
|
|
#99 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
���� ���������� ��������
Код:

|
|
|

|
|
|
#100 |
|
Форумчанин
Регистрация: 10.01.2020
Сообщений: 377
|
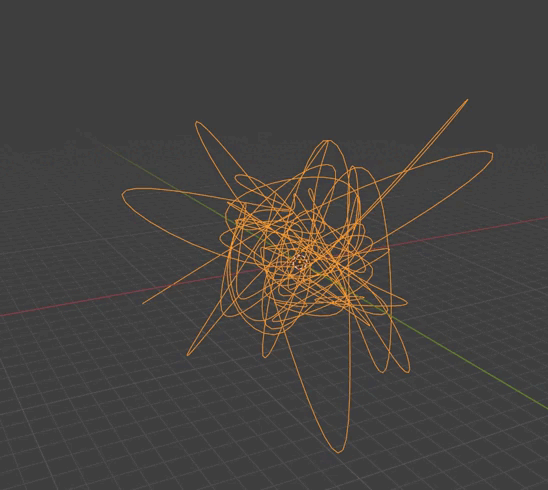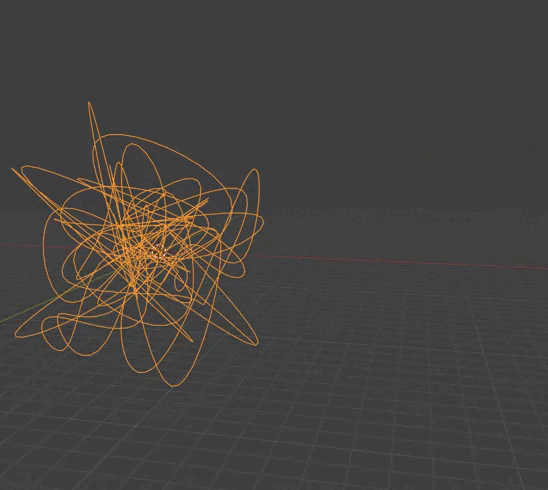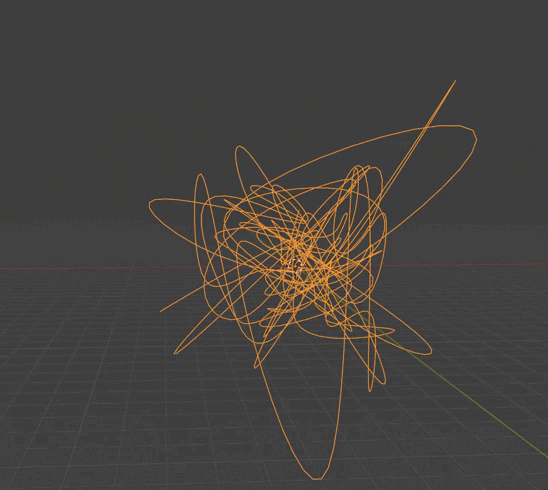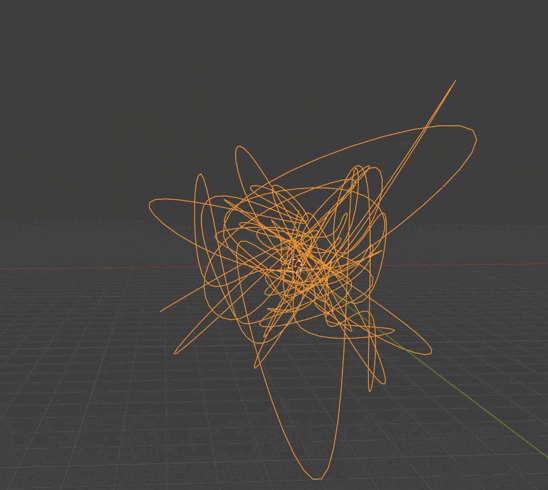
Изогнутая линия с сохранением
Код:
|
|
|

|
 |
|
 Похожие темы
Похожие темы
|
||||
| Тема | Автор | Раздел | Ответов | Последнее сообщение |
| помогите с генератором слов | Мой повелитель | Общие вопросы C/C++ | 6 | 27.02.2016 23:46 |
| Зарубежные микроконтроллеры с встроенным ШИМ-генератором | MyLastHit | Компьютерное железо | 6 | 22.10.2013 14:33 |
| написание генератора фракталов Жюлиа | kyzmich2370 | Visual C++ | 1 | 06.11.2012 09:57 |
| Помогите с генератором чисел на Pascal | vadmaruschak | Помощь студентам | 6 | 13.09.2009 17:06 |
| Игры фракталов на VB | Kail | Свободное общение | 1 | 29.05.2009 09:30 |